13.4 — Images Formed by Lenses

Lenses are optical devices made of transparent material that refract light to form images. There are two primary types of lenses:

1. Convex (Converging) Lenses: Thicker at the center to bring parallel light waves together to converge at a focal point
2. Concave (Diverging) Lenses: Thinner at the center to spread parallel light waves outward as if originating from a focal point

This contrast is depicted through the image below:

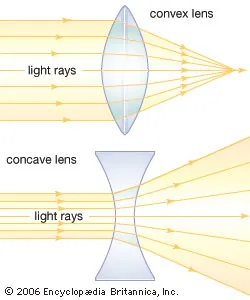
An infraction:

• Real Image: when light rays cross to form an image and the image can be seen on the screen
• Virtual Image: When light rays do not cross; instead they diverge as if they came from the image., and the image cannot be seen on the screen.
• Upright Image: when the image has the same orientation as the object
• Inverted Image: when the image orientation has been flipped on both axes
• Enlarged Image: when the image appears larger than the object
• Reduced Image: when the image appears than smaller than the object

Convex (Converging) Lens

Converging lenses refract parallel light rays inward to meet at the focal point. They can form either real or virtual images depending on the object’s position relative to the focal length ($f$). The focal length is the property of the lens and depends on the material (index) and the shape.

Refraction Patterns

There are multiple different reflection patterns with lenses. Here are diagrams and descriptions of each.

Object Placed Behind Focal Point

1. A ray that starts at the object and travels parallel through the principal axis will refract through the focal point on the opposite side of the lens
2. Conversely, a ray that starts from the object and goes through the closer focal point will refract through the lens and end up as a ray parallel to the principal axis on the other side.

The image will form where these two rays cross, and this image will be real, inverted, and reduced:

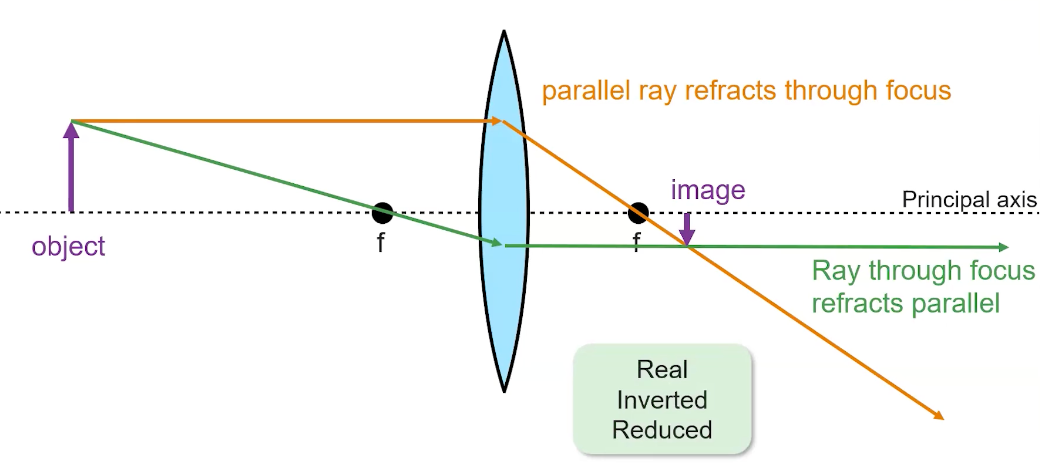
Object Placed Between Focal Point and Lens

1. Rays parallel to the axis will still start at the object, go through the lens, and intersect the focal point on the opposite side of the lens.
2. Other rays will go straight through the center and do not refract as the incident angle is 90 degrees

In this case, the two rays don’t cross, so we’ll need to extend the lines backwards and find their intersection point. This image will be virtual, upright, and enlarged:

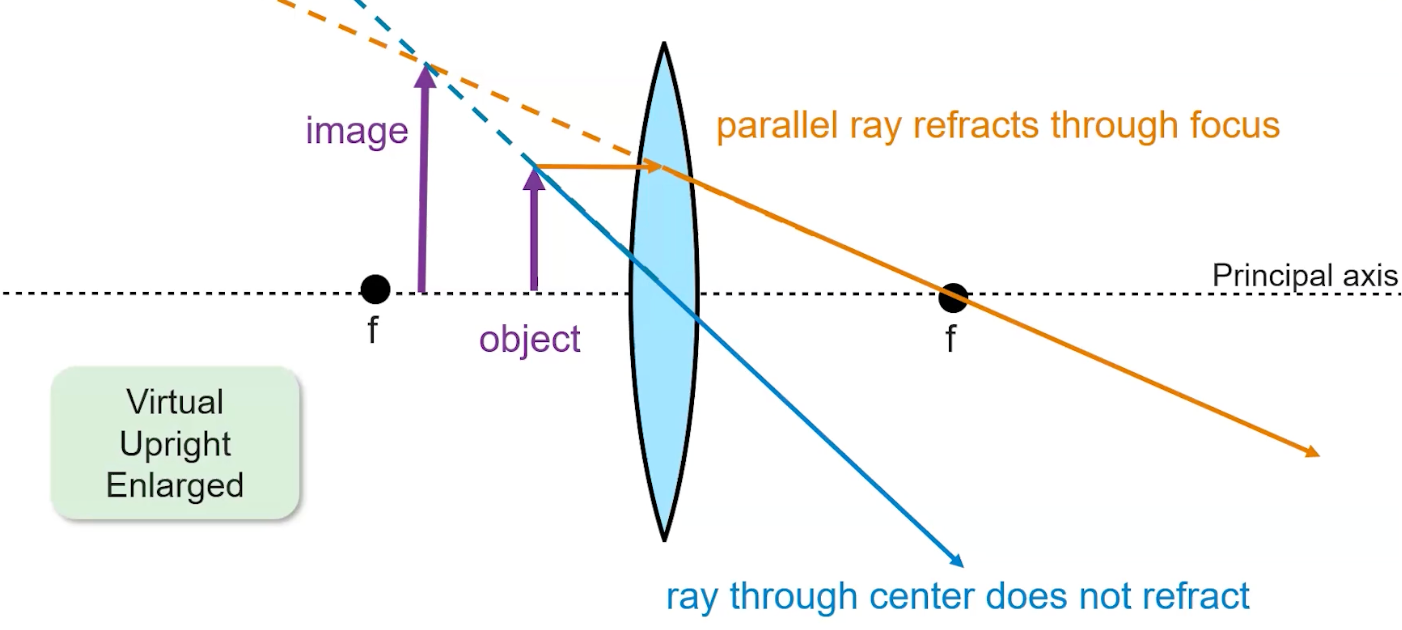
Concave (Diverging) Lens

Diverging lenses cause parallel light rays to spread outward, appearing to diverge from a focal point. These lenses always form images that are:

1. Virtual
2. Upright
3. Reduced

The focal length of a concave lens is always negative.

Refraction Patterns

1. Rays parallel to the principal axes will refract as if they came from the focus behind the lens
2. The second ray which goes through the center of the convex lens will go straight through as it is not refracted

These two rays intersect in between the focal point and the convex mirror, and this image will be virtual, upright, and reduced:

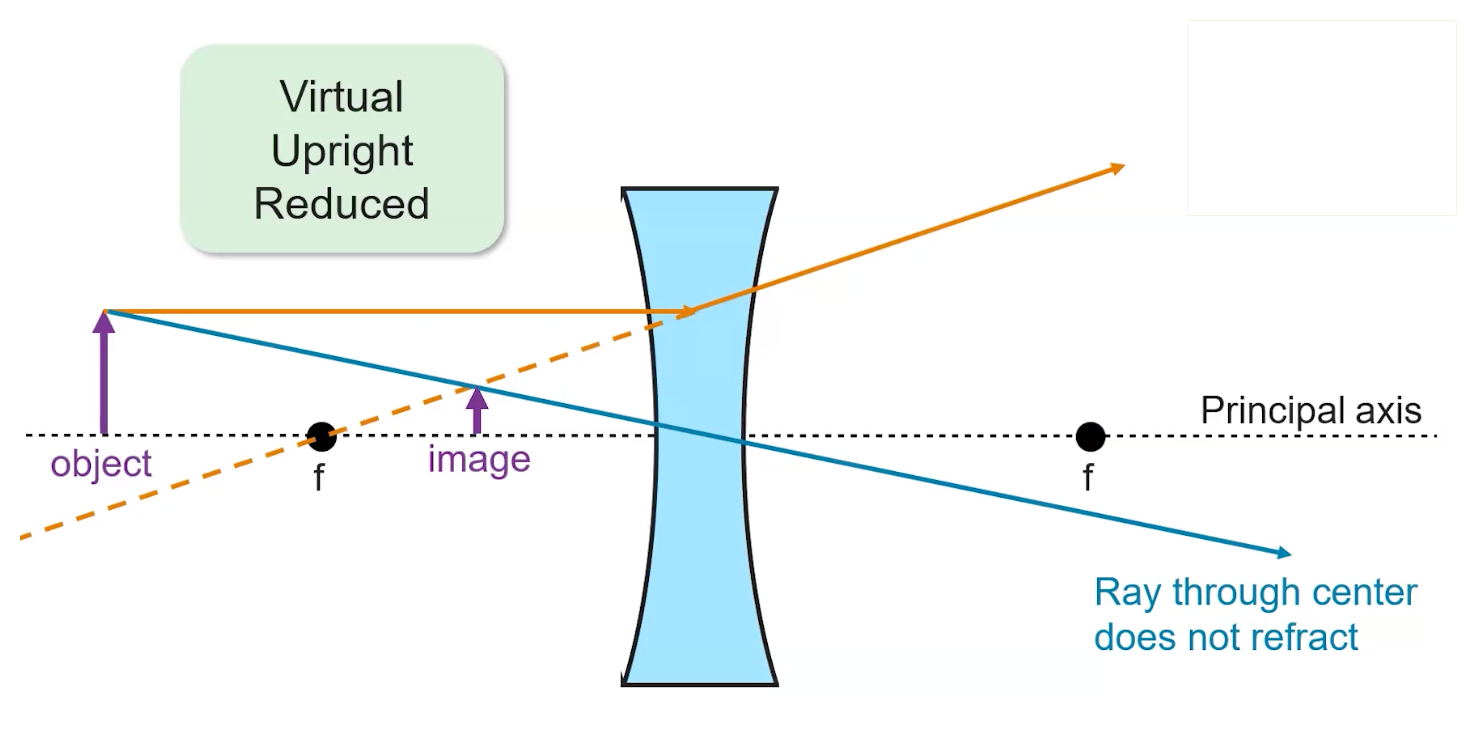
Thin-Lens Equation

The thin-lens equation is identical to the mirror equation but used for lenses: $\frac{1}{f}=\frac{1}{d_o}+\frac{1}{d_i}$ where:

• $f$ is the focal length
• $d_o$ is the object distance
• $d_i$ is the image distance

Magnification Equation

We can also use the same magnification equation which we used in mirrors. $M$ refers to the ratio of the image height to the object height, and will help us calculate the size of the image. If magnification is greater than 1, then the image is enlarged; otherwise, the image is reduced.

$|M|=|\frac{h_i}{h_o}|=|\frac{d_i}{d_o}|$ where:

• $h_i$ is the image height
• $h_o$ is the object height
• $d_i$ is the image distance
• $d_o$ is the object distance

---

The following table describes our four possible cases:

	Positive	Negative
Focal Length ($f$)	Convex Lens	Concave Lens
Image Distance ($d_i$)	Real Image	Virtual Image
Image Height ($h_i$)	Upright Image	Inverted Image