Wave Interference is essentially the interaction of two or more wave pulses or waves—where they travel through each other and overlap rather than bouncing off. The resulting overlapping of waves can be calculated by adding their displacements, which is known as superposition.
Superposition
Just like we learned in AP Physics 1, constructive interference is when we add the amplitudes together, and destructive interference is where the amplitudes add up to be zero. Here are some examples:
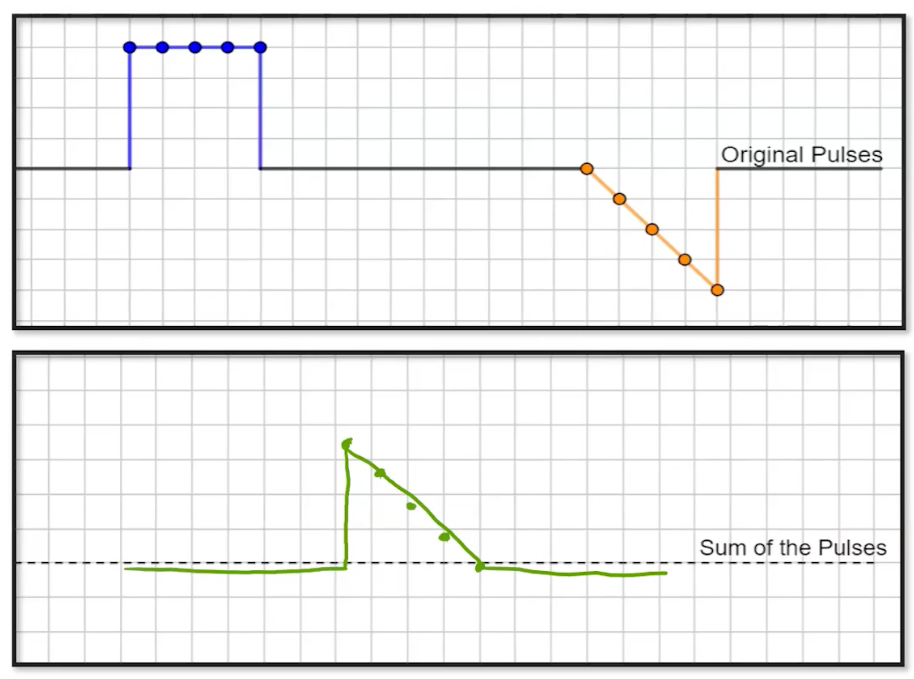 | 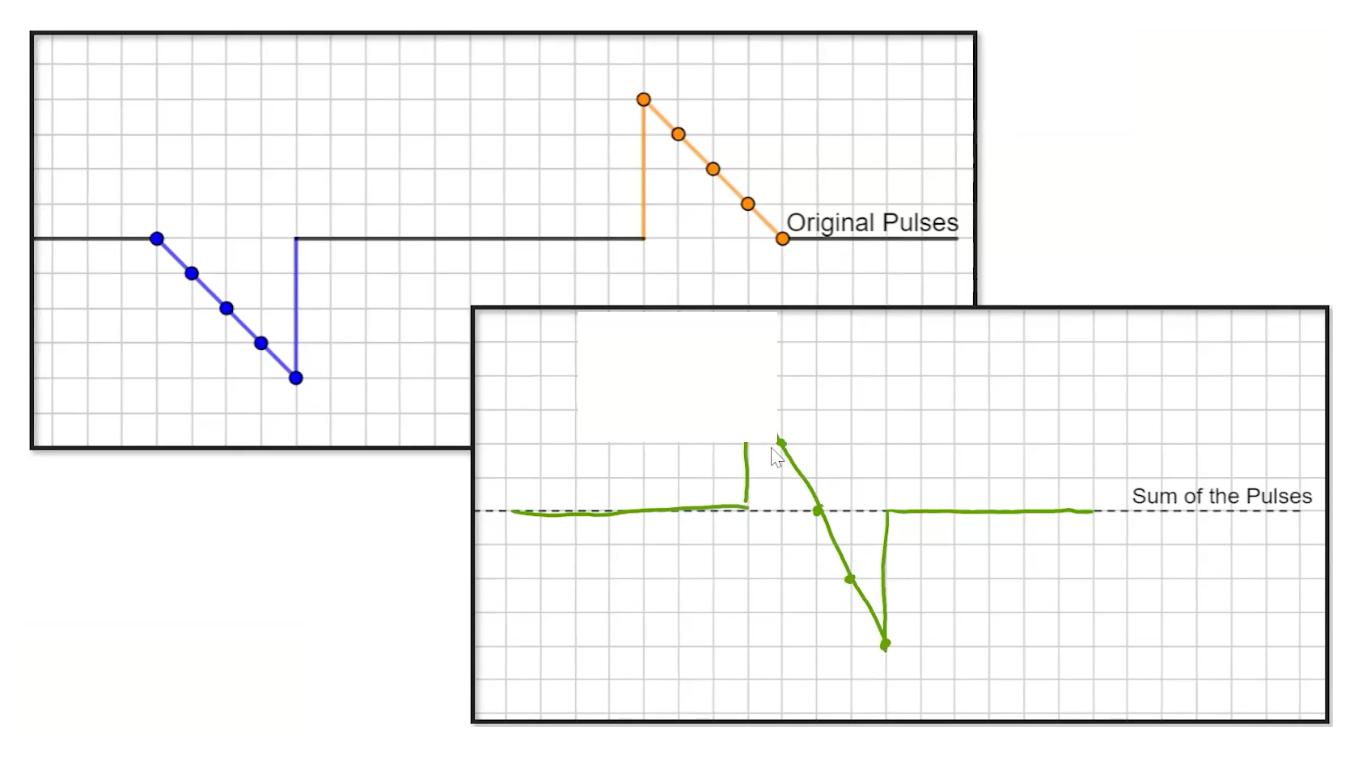 |
|---|---|
 | 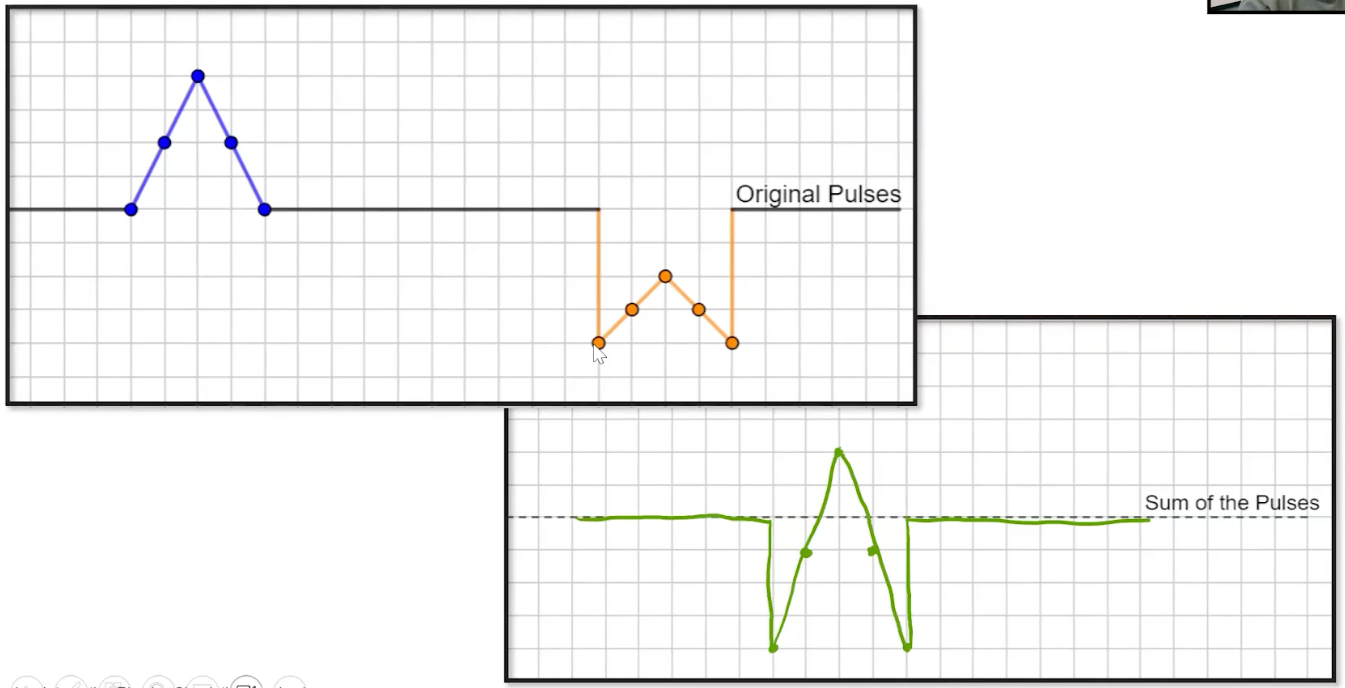 |
| When we superimpose waves, we get radically different frequencies. For example, while a sound wave of 440 Hz is quite similar to 441 Hz, the result of superimposing them is $ | 441 - 440 |
Standing Waves
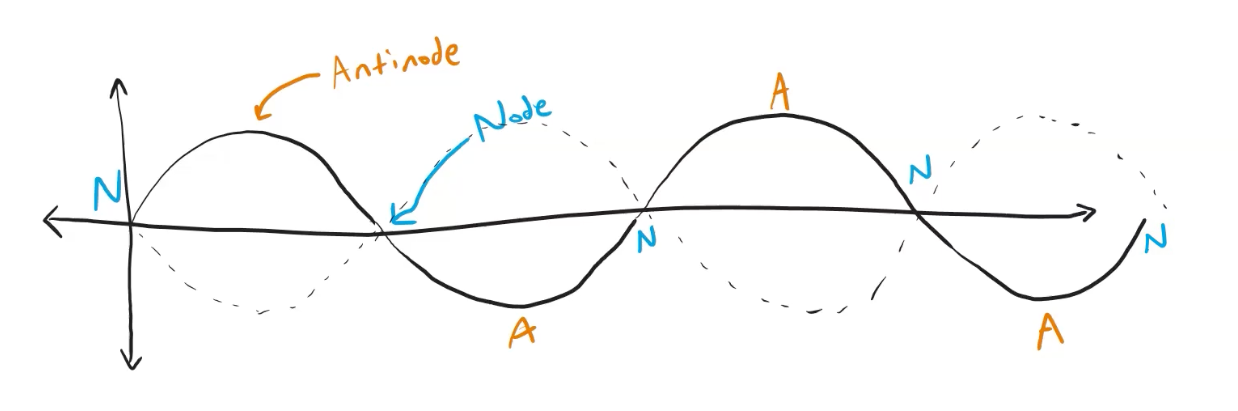
A standing wave usually results from the interference of two waves that are confined to a region and travelling in opposite directions. These standing waves have nodes and antinodes. A node is a point on a standing wave where the amplitude is equal to zero, while an antinode is a point on a standing wave where the amplitude is at an absolute maximum
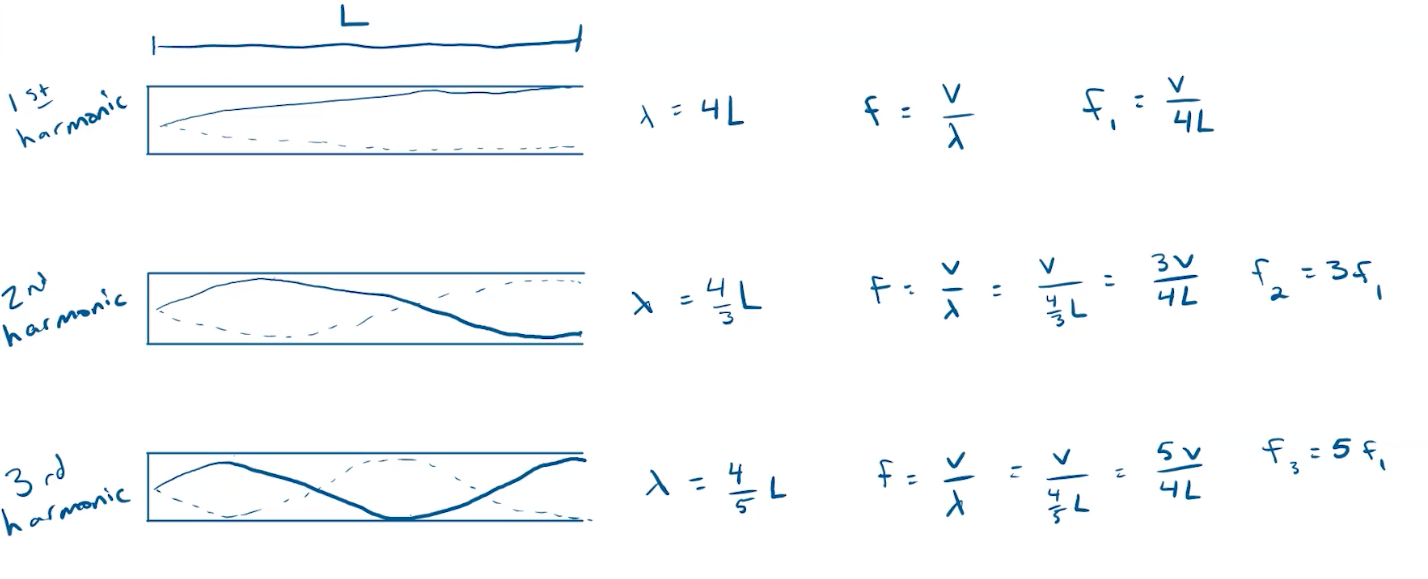
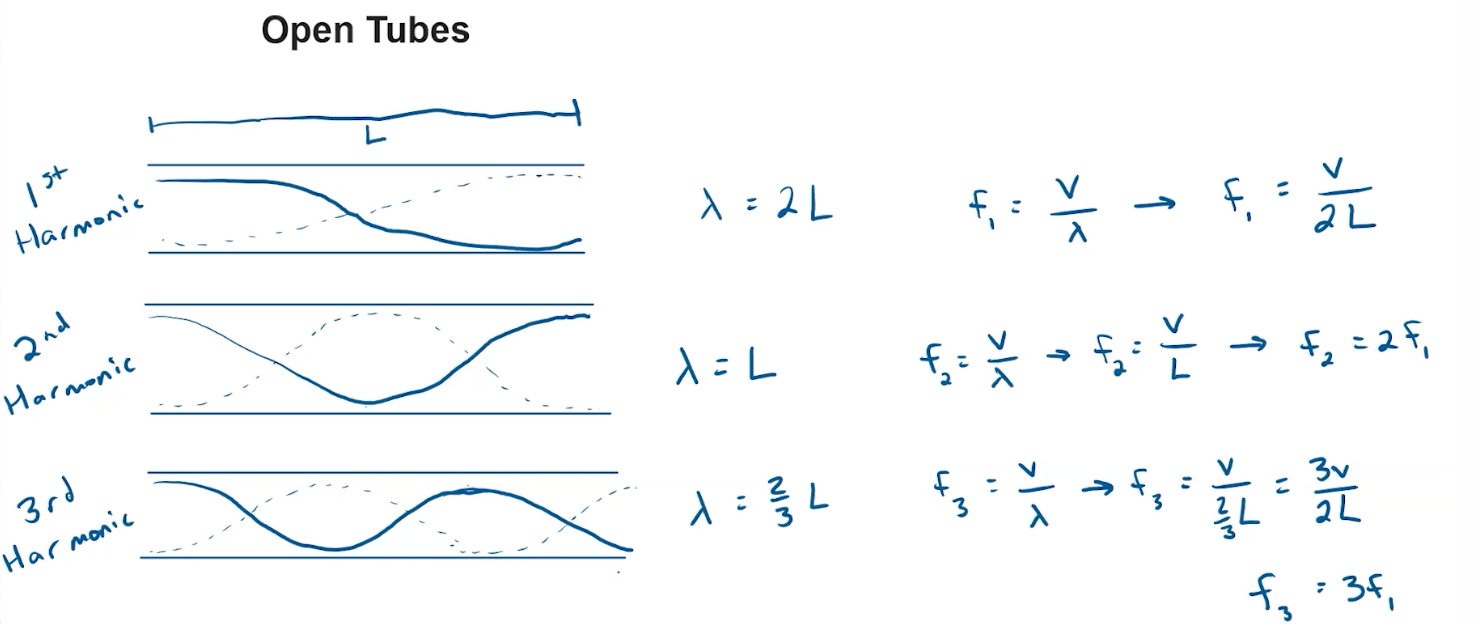
Open Tubes
In open tubes, the first harmonic is created when which means that half of the wavelength fits in the tube. Correspondingly, the second harmonic is created when and the third harmonic is created when . From the below chart, you can see the relationship between the frequencies of the different harmonics (the integer coefficient increases by 1 each time):
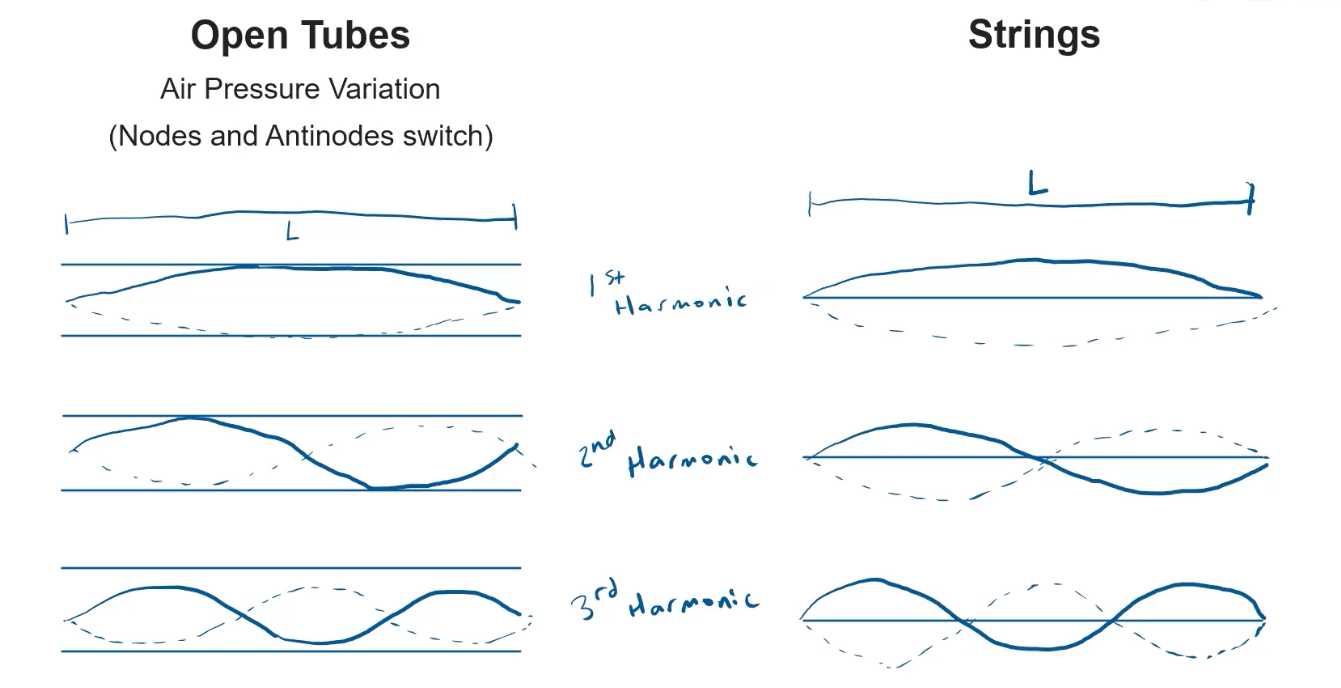
Open tubes have the same harmonic structure as standing waves on a string. Open tubes have an air pressure variation which is where the nodes and antinodes switch, and this variation is exactly identical to the harmonic structure of fixed strings:
Fixed End Tube
When waves in a fixed end tube reach the closed end, they reflect back with their amplitude in the inverse direction. Thus, a wave in a closed end tube will have its pulses reflect and create another wave, which correspondingly creates the interference and superposition.
For closed tubes, the harmonics are as follows: the first harmonic will have , the second harmonic will have , and the third harmonic will have . The corresponding frequencies will have integer coefficients increasing by 2 each time: