13.2 — Images Formed by Mirrors

Mirrors are generally one-sided.

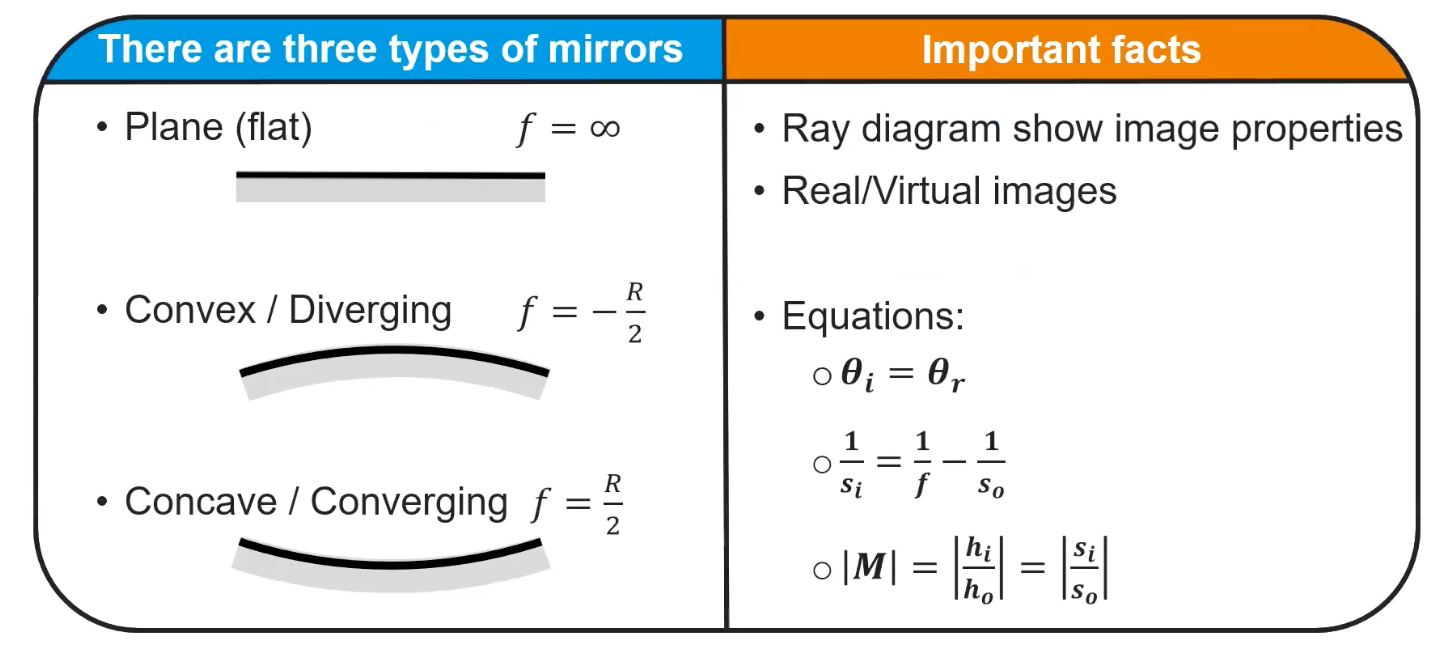
• Plane Mirror: Flat mirror with specular reflection. Ex: bathroom mirror
• Curved Mirror: Concave/convex with a single mirrored side. Imagine using only a section of the sphere, and one is curved inward and one outward

On the left is a plane mirror, and the two mirrors on the right are a part of a spherical/curved mirror.

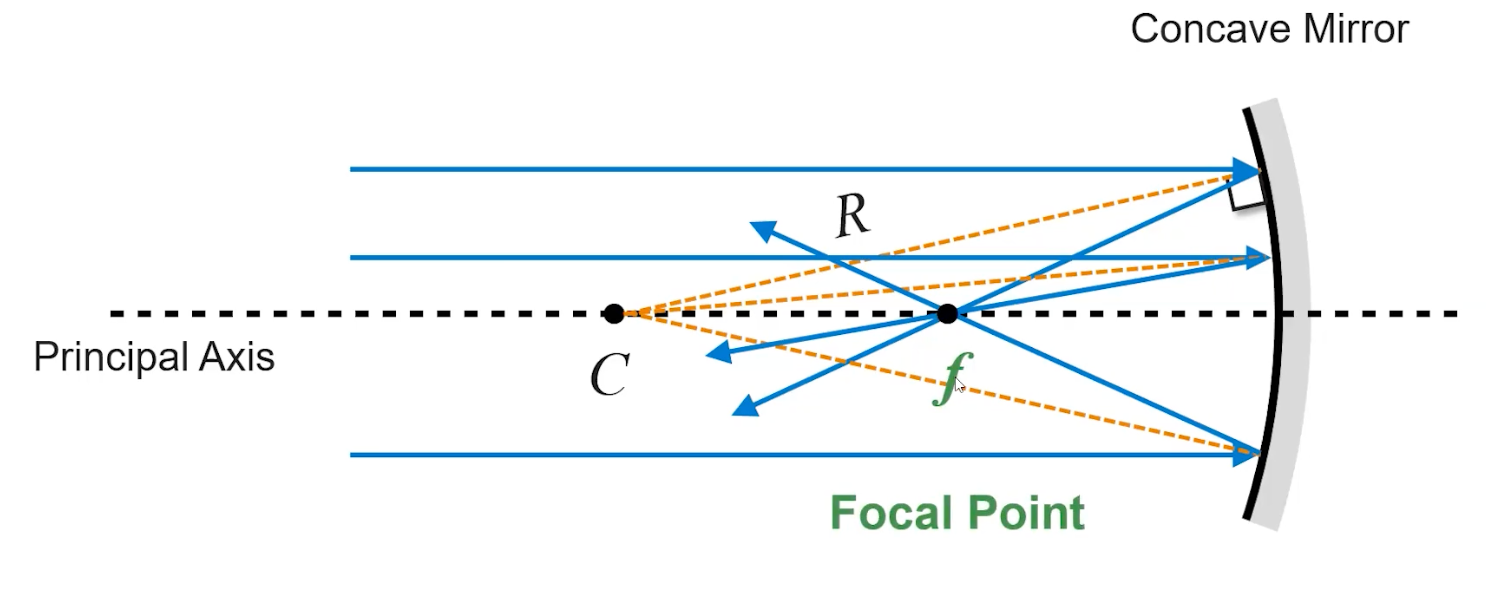
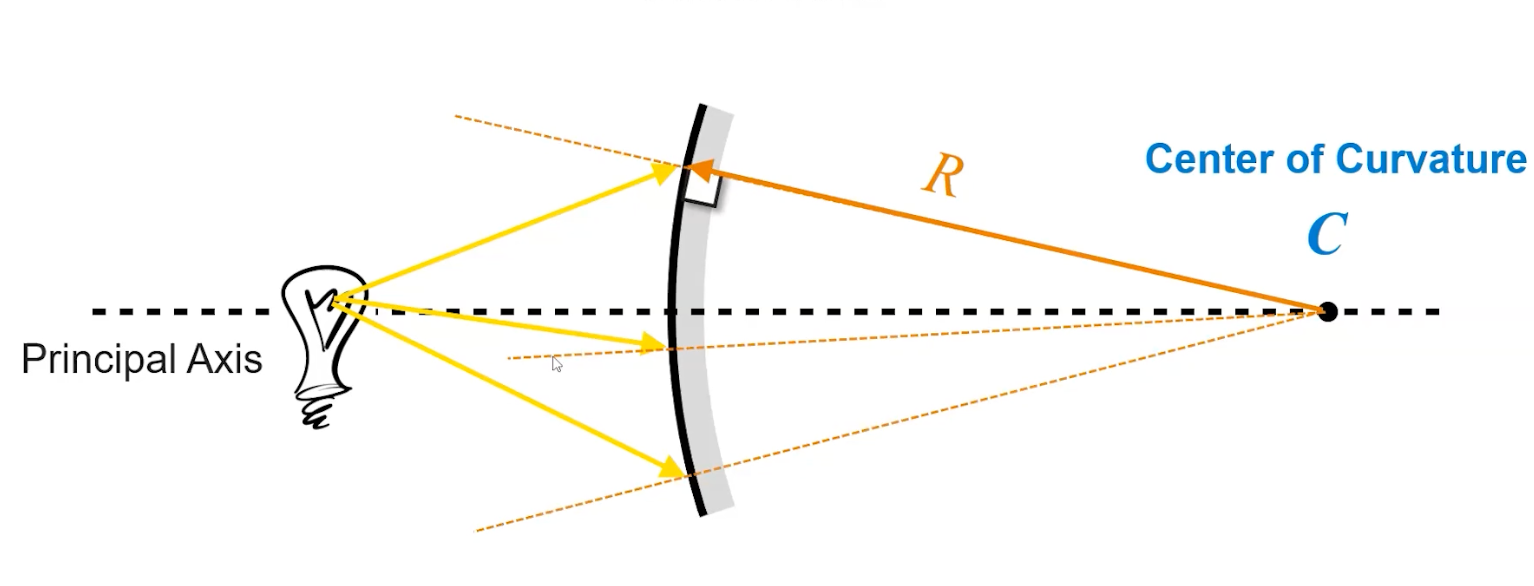
The Center of Curvature ($C$) is the point which represents the center of the circle which has the radius of the mirror. It is always perpendicular to the mirror and serves as a normal line to the mirror.

The Principal Axis is the line of symmetry of the mirror. The focal point ($f$) is positioned on the principal axis, halfway between the center of curvature and the mirror. As a result, the focal length of a spherical mirror is always half of the radius. The below image shows the center of curvature, the principal axis, and the focal point for a concave mirror. The image below shows the same for a convex mirror.

Flat / Plane Mirror

Plane mirrors produce only one type of image

1. Upright and virtual images
2. Images that are the same size as the object
3. Images that are the same distance behind the mirror as the object is in front of the mirror

This means that plane mirrors have a focal length of $\infty$. Similarly, they have an equal opposite distance which means $s_i=s_o$. Finally, since the image is virtual, their $f$ will be negative.

Concave (Converging) Mirror

Concave mirrors produce both real and virtual images, depending on the location of the object in relation to the focal point.

The three main cases are:

1. The object is placed in between the focal point and the mirror: in which case it creates a virtual image ($-f$). The size and distance of the virtual image will change based on the size and distance of the object.
2. The object is placed at the focal point: in which case, no image is formed.
3. The object is placed behind the focal point: In which case, a real image is formed but it is inverted. The size and distance of the real inverted image will change based on the size and distance of the object.
   • When the object is placed exactly at the center of curvature, we will have an identical real inverted image placed right beneath it
   • When the object is placed at an infinite distance away, the image will be placed exactly at the focal point

Reflection Patterns

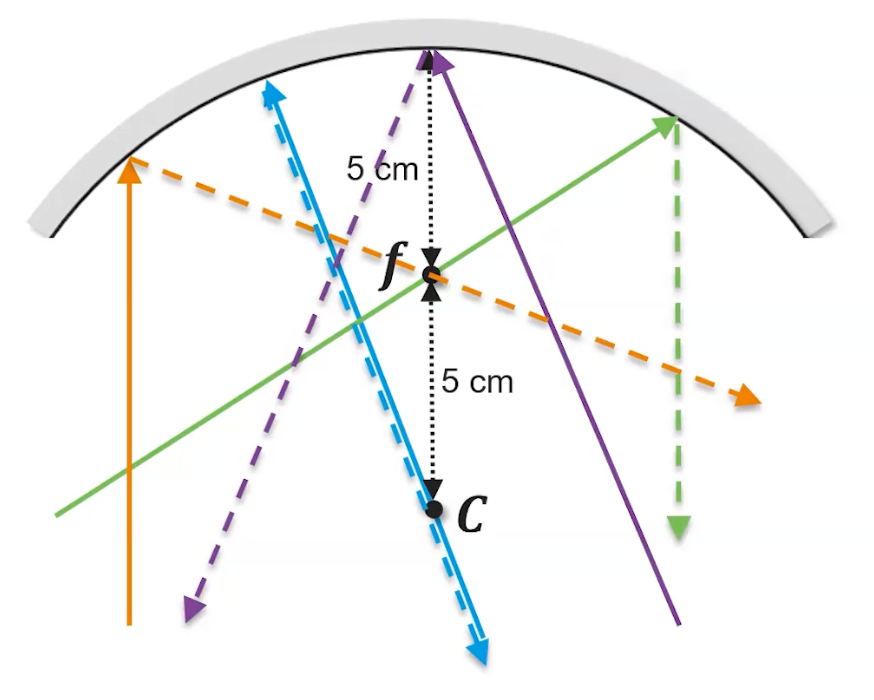
1. Vectors originating from the center of curvature will reflect off the mirror and return back to the center. This is represented by the blue vector in the below image.
2. Vectors that are parallel to the principal axis will rebound and intersect through the focal point. This is represented by the orange vector in the below image.
3. Vectors that are directed towards the focal point will reflect and follow the direction of a vector that is parallel to the principal axis. This is represented by the green vector in the bill of image.
4. Vectors that hit the center of the mirror will follow the large reflection and reflect at an equal angle on the opposite side of the principal axis. This is represented by the purple vector in the below image.

Convex (Diverging) Mirror

Convex mirrors also form only one type of image:

1. Upright and virtual images
2. Images which are smaller than the object
3. Images that are behind the mirror

This means that, since the image is virtual, their $f$ will be negative. Essentially, convex mirrors also have a focal point, but it’s referred to as a virtual focus ($-f$) because light doesn’t reflect back to this point but instead away from the mirror.

Similar to concave mirrors, convex mirrors also have a center of curvature and a principal axis. However the center of curvature is on the backside of the mirror (which is not where light is coming from). As a result, light rays will not reflect back to the light source as their normal lines will be on the opposite direction.

Reflection Patterns

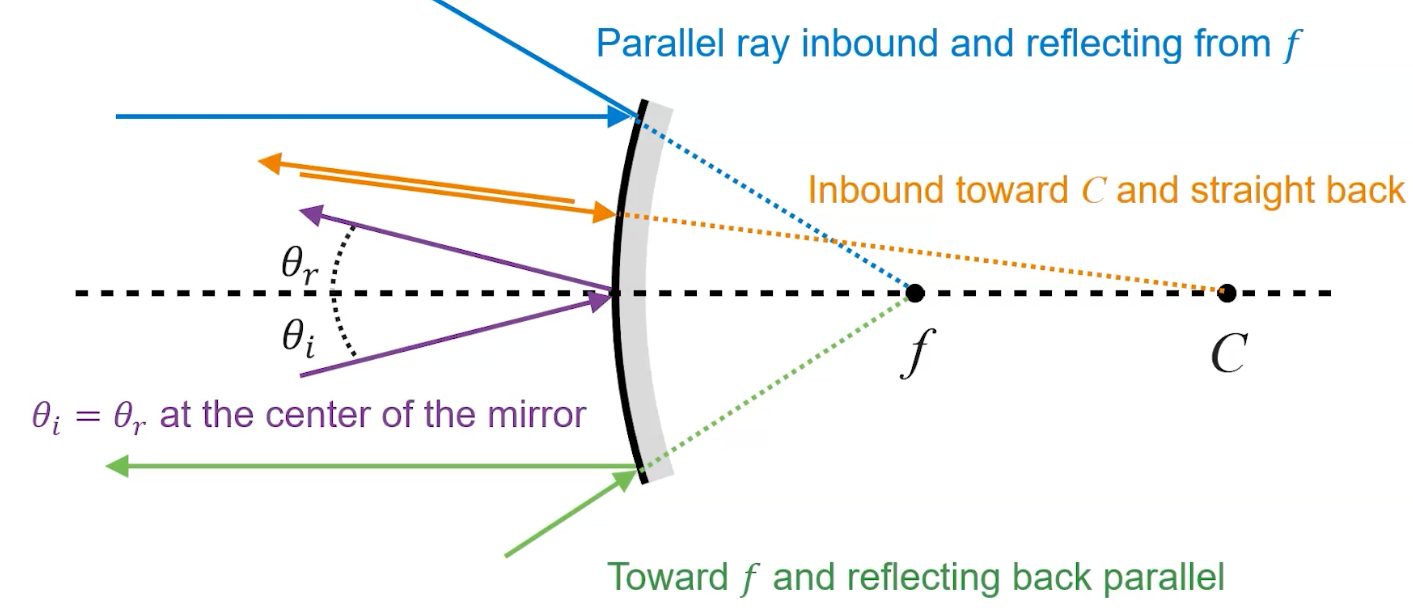
1. Light rays that are parallel to the principal axis will rebound and follow the vector that begins on the focal point of the mirror. This is illustrated through the blue vector in the lower image.
2. Conversely, vectors that are directed towards the virtual focal point will reflect back and follow the vector that is parallel to the principal axis. This is illustrated through the green vector in the below image.
3. Light rays that hit the center of the mirror will follow the large reflection and reflect at an equal angle on the opposite side of the principal axis. This is illustrated by the purple vector in the below image.
4. Light rays directed towards the center of curvature will reflect exactly in the direction they originated from. This is illustrated by the orange vector in the below image.

A virtual image is essentially where the light rays seem to reflect/emit from, but since this image doesn’t actually exist, it cannot be depicted on a screen.

Image Formation

• Almost all light rays travel in straight lines
• Our eyes see object along these lines
• All we need is light to see an image
• We can use geometry to locate an image

Mirror Equation

There is a fundamental Mirror Equation as follows $\frac{1}{s_i}=\frac{1}{f}-\frac{1}{s_o}$ where:

• $f$ is the focal length ($\infty$ for plane mirrors)
• $s_i$ is the image distance ($+$ if real and $-$ if virtual)
• $s_o$ is the object distance

To remember:

1. Since focal length is $\infty$ for plane mirror, we know $s_i=-s_o$
2. A negative image distance means the image is behind the mirror and is a virtual image.
3. Conversely, a real image is where the light bounces off the mirror and the image is formed in front of the mirror. This is when we have a real image.

Magnification Equation

There also exists a magnification equation: $|M|=|\frac{h_i}{h_o}|=|\frac{s_i}{s_o}|$ where:

• $M$ is the magnification
• $h_i$ is the image height (size)
• $h_o$ is the object height (size)
• $s_i$ is the image distance
• $s_o$ is the object distance

To remember:

1. Since $s_i=-s_o$ for plane mirrors, we know that $M=1$ which means a plane mirror always reflects an image of the same size (and the same distance away).

Summary