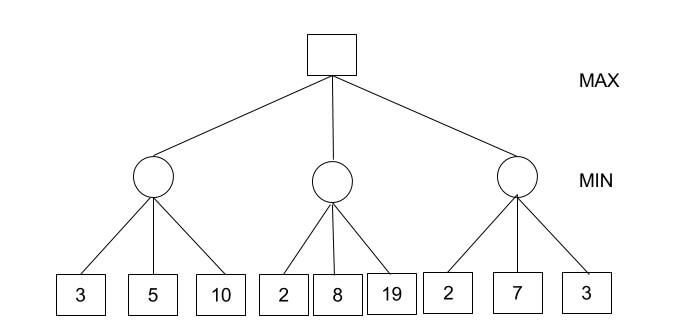
Alpha-Beta Pruning reduces the number of nodes that are evaluated by a minimax algorithm in a search tree. Essentially, when looking at a graph to optimize the output of some action, alpha-beta pruning eliminates nodes when they have been found to be worse than any previously examined move. Taking Depth First Search (DFS), alpha-beta pruning would entirely ignore certain branches if their parent nodes show that navigating down the branch would not lead to a better final outcome. It makes it less computationally intensive to find the optimal move in a search tree.
These search trees are primarily present in two-player games like chess, checkers, etc. Each node in the search tree represents a potential game tree and they are assigned a numeric score that determines the value of the outcome to the player if they play that move. The algorithm maintains two values, alpha and beta, which represent the minimum and maximum score that the maximizing player is assured of. For each branch, if the maximum score (beta) becomes less than the minimum score (alpha), further descendants of the node do not need to be evaluated anymore.