Backpropagation is an algorithm used to train neural networks by enabling them to learn from data and adjust the weights of their network. Modern backpropagation for training multi-layer neural networks was introduced by David Rumelhart, Geoffrey Hinton and Ronald Williams in a paper called “Learning representations by back-propagating errors”.
It starts with the forward pass, where data is inputted into the neural network. It moves layer by layer, and at each layer, inputs are multiplied by weights and passed through an Activation Function and produce outputs that feed into the next layer. Finally, the output layer provides a prediction based on the current weights.
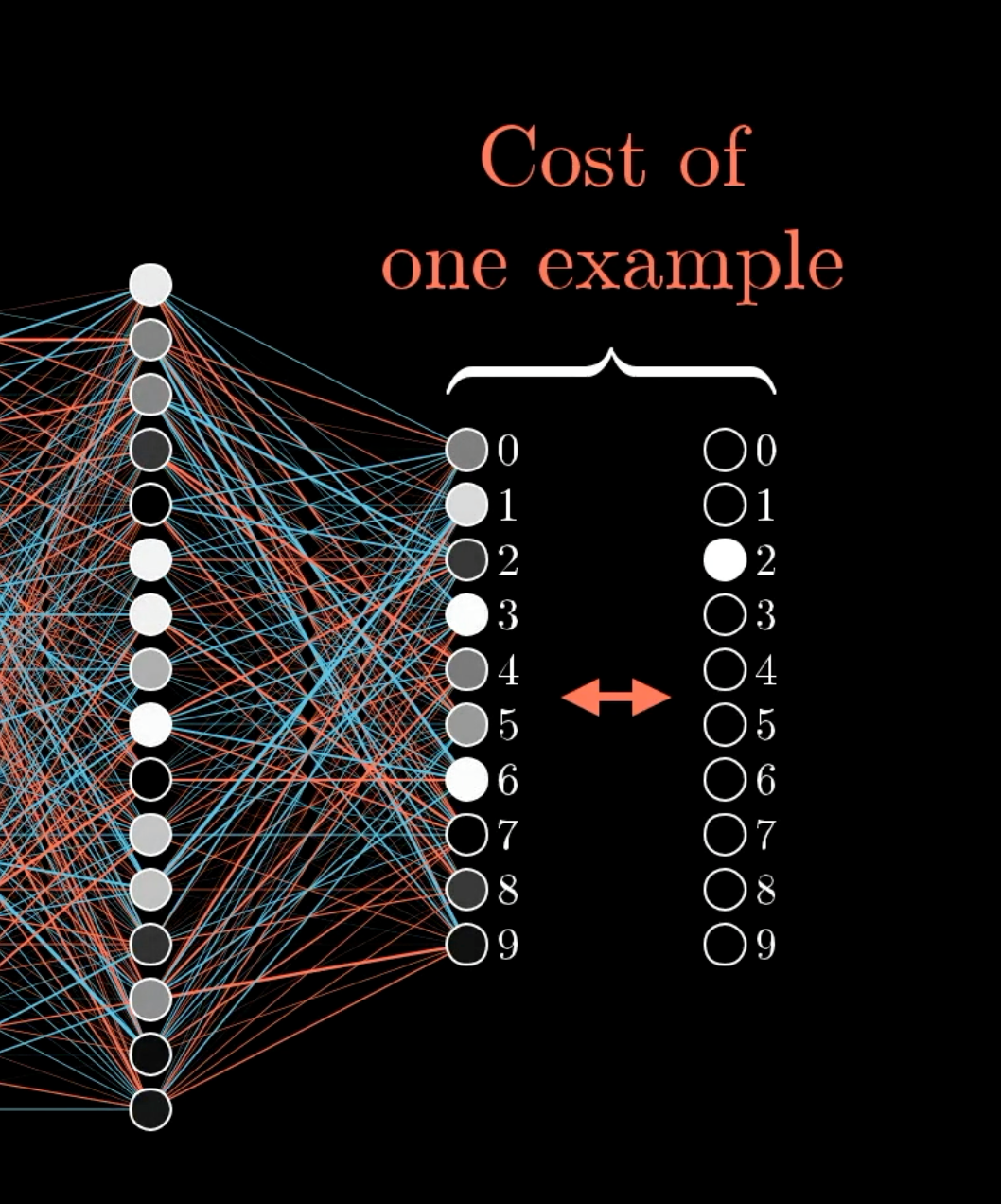
After getting the prediction, backpropagation compares the actual target value using a loss function, representing how far off the network’s prediction is from the target. For example, in the below example, we sum up the calculated probabilities of all wrong predictions and that represents the loss of that training iteration.
Now, backpropagation uses this calculated error to adjust the weights in the network by propagating it backward, starting from the output layer back to the input layer. This involves calculating the gradient of the loss (Gradient Descent) with respect to each weight (apparently this uses the chain rule of calculus!). The gradient tells us the direction and magnitude of change needed to minimize the error for each weight.
Once we have the gradients, backpropagation slightly adjusts the weights in each direction and that will reduce the loss. The amount we adjust each weight is scaled by a learning rate, the hyperparameter that determines the step size for weight adjustments. A small learning rate means small adjustments and slower learning, while a higher learning rate means larger adjustments. This can speed up learning but might also risk overshooting the optimal solution because taking larger steps while traversing the gradient might lead to missing a local minimum.