Gradient descent is an optimization strategy that is used to train data models. It is a function that continuously tweaks its parameters to minimize a given loss function to its local minimum. Essentially, it is used to find the specific weights and biases (and other parameters) to minimize the final cost function as far as possible.
Gradients
A gradient measures the change in all the weights compared to the change in error. Essentially, it is the slope of a function. The higher the gradient, the steeper the slope, and the faster the model can learn. When the slope is zero, the model stops learning.
Convex Function
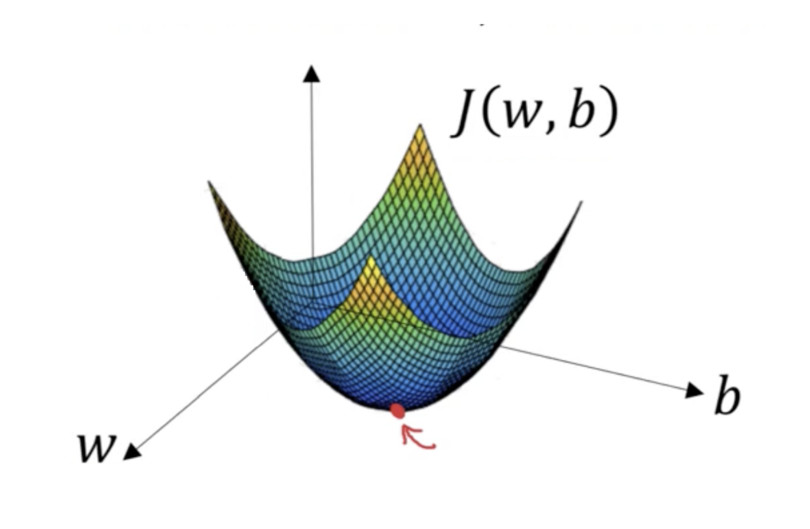
In the below image, w and b refer to the weights and biases of the function, and refers to the output of the loss function with those weights and biases as inputs. The gradient descent algorithm seeks to minimize the loss function, essentially finding the lowest point in the convex gradient.
Learning Rate
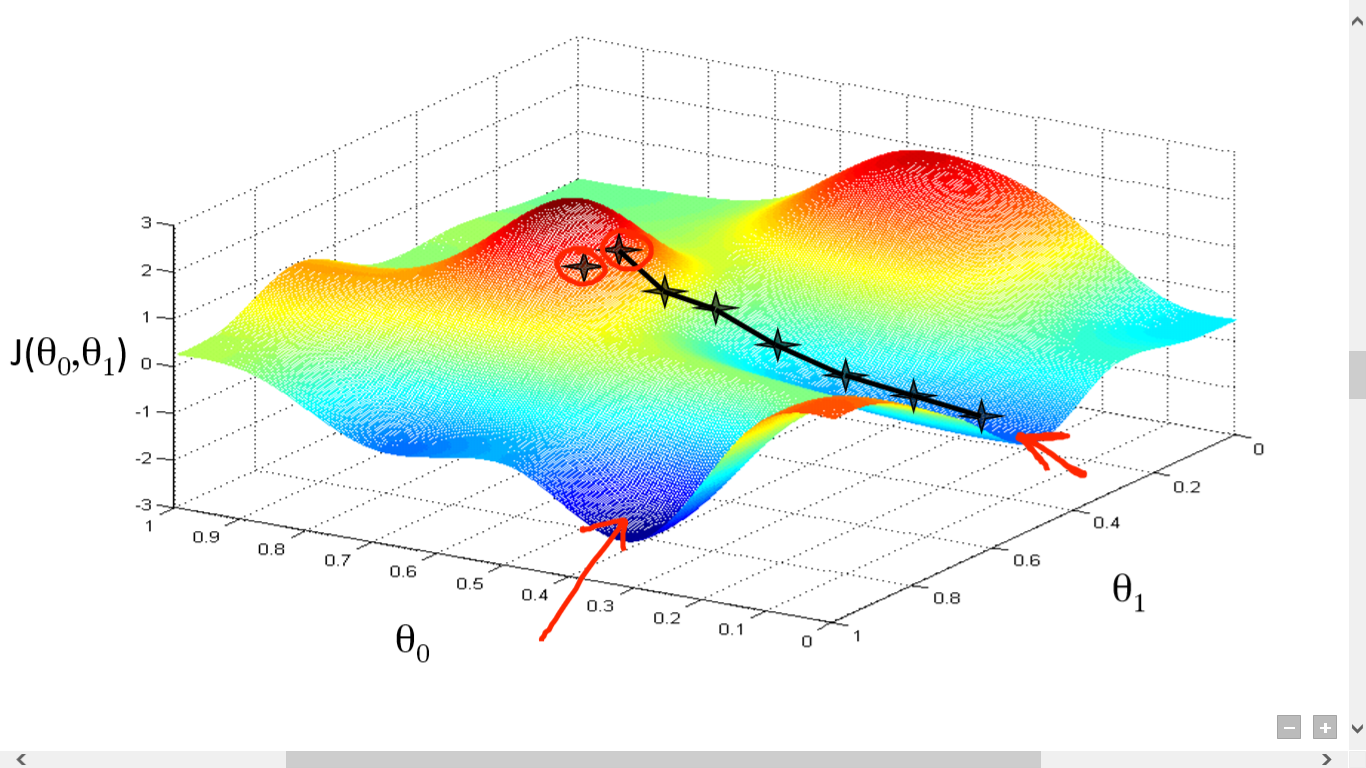
The gradient descent algorithm essentially makes steps into the direction of the local minimum, which is represented by the gradient output of the loss function. The size of these steps is determined by the learning rate hyperparameter, which decides how fast or slow the algorithm will move towards the optimal weights.
One needs to ensure that the learning rate isn not too low nor too high. If the steps are too big, it may not reach the local minimum because it will keep bouncing back and forth between positive and negative slopes. If the steps are too small, it will eventually reach a local minimum but there might be much more optimal (global) minimums.
