Potential Problems
Multicollinearity
Multicollinearity occurs when there are high correlations between two or more independent variables in a linear regression module. For linear regression, we want a good correlation between the independent variables and the output. Multicollinearity leads to less reliable statistical inferences (estimates) and becomes highly sensitive to random errors.
Overfitting
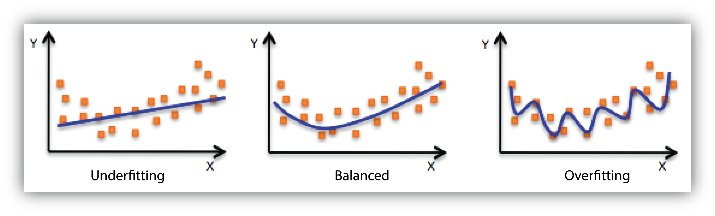
A linear regression model is overfit when it is too accurate to the provided sample data and no longer serves to provide realistic estimates for the dependent variable. This happens when the model is too complex and it essentially memorizes the training dataset.
Underfitting
A linear regression model is underfit when it is too general to the provided sample data and does not provide realistic estimates for the dependent variable. This happens when the model is too simple and does not capture the dataset trends.
Potential Solutions
Regularization
To address problems with overfitting, regularization techniques are used (L1 or L2).
L1 Regularization, also known as Lasso Regression (Least Absolute Shrinkage and Selection Operator), adds the absolute value of the magnitude of the coefficient as a penalty term for the loss function. Essentially, since the model is overfitted to the training data, L1 Regularization removes some features (coefficients) from the model so it ignores some features of the data.
L2 Regularization, also known as Ridge Regression, adds the squared magnitude of the coefficient as the penalty term to the loss function. Essentially, L2 Regularization shrinks some features (coefficients) but still doesn’t set them to zero.
Suppose you are predicting house prices based on features like size, number of bedrooms, and location:
- Without Regularization: The model uses all features, but it might overfit the training data (like memorizing exact prices without understanding general trends).
- With L1 Regularization (Lasso): The model might decide that the number of bedrooms isn’t that important and set its coefficient to zero, simplifying the model (like ignoring the number of bedrooms when predicting prices).
- With L2 Regularization (Ridge): The model uses all features but reduces their influence slightly to prevent overfitting (like using a little bit of each feature to make a prediction).
Use L1 Regularization when you suspect that only a few features are important for your model and you want to automatically select those features by shrinking the rest to zero. Use L2 Regularization if you have many correlated features and you believe all of them contribute to the prediction to some extent.